Nadácia Tatra banky podporila projekt ClouDiaDAQ!
Projekt ClouDiaDAQ (Diabetic Data Acquisition via Cloud) si dáva za cieľ preskúmať možnosti a prínosy zdieľania CGM dát v reálnom čase. Projekt nadväzuje na predchádzajúci projekt DiaDAQ, ktorý bol podporený Nadáciou Tatra banky v rámci grantového program E-Talent 2013. Autorskí tím má aj vďaka tomu dostatok skúseností so získavaním a spracovaním CGM dát. Nemáme však vedomosť o tom či na sa na slovensku niekto zaoberal zdieľaním CGM dát v reálnom čase.
Prvý komerčne dostupným produktom umožňujúcim zdieľanie CGM dát v reálnom čase je Dexcom SHARE. Na trh v USA bol uvedený nedávno, v októbri 2014. Je pravdepodobné, že v najbližšom čase bude tento produkt dostupný aj v Európe. Avšak v čase prípravy tohto projektu Dexcom SHARE nie je dostupný v Európe. Aplikácie využívajúce tento systém sú momentálne dostupné len pre operačný systém iOS, a nie sú opensource.
Približne pred rokom sa objavila možnosť sťahovať dáta z monitora CGM systému, častejšie nazývaného prijímač (značky Dexcom), prostredníctvom mobilného zariadenia s operačným systémom Android. Skupina nadšencov našla spôsob ako využiť súčasti originálneho softvéru pre sťahovanie dát z monitora tak aby riadenie sťahovania týchto dát bolo možné aj bez originálneho softvéru (a aj na iných operačných systémoch). Projekt sa nazýva Nightscout, umožňuje zdieľanie CGM dát prostredníctvom Cloud-u (internetu) v reálnom čase a je open-source (http://nightscout.github.io/).
V rámci projektu ClouDiaDAQ plánujeme využiť Nightscout ako nástroj pre zdieľanie CGM dát cez internet v reálnom čase.
19. 12. 2014
Senzor pod makro objektívom
Senzor Enlite (Medtronic) pod makro-objektívom a pred makro-objektívom v improvizovanom (v rámci možností aj keď nie práve najlepšie) „light box-e“.
MT
2. 12. 2014
O rozpoznaní nespoľahlivého merania (senzora)
Nominálna dĺžka používania senzora Enlite (Medtronic) je 6 dní (podľa výrobcu). Počas tohto času by mal merať dobre. Avšak správanie senzora sa mení. Z rôznych príčin. Senzor má svoju životnosť a kvalita merania pomocou senzora sa s časom jeho používania mení. Postupom času sa zhoršuje (väčšinou). Pre úspešné používanie CGM systému je potrebné všímať si tieto zmeny. Umožní to rozoznať či je senzor v poriadku a či meria tak ako má, alebo meranie z nejakých príčin zlyháva a je nespoľahlivé.
Ukazovateľmi stavu senzora by mohli byť „zašumenosť“ meraného priebehu glukózy zo senzora a teda „zašumenosť“ ISIG signálu a zároveň samotná veľkosť ISIG signálu. Ukážme na dátach od jedného subjektu. Počas posledných zhruba dvoch mesiacov subjekt použil 5 snezorov.
Ukazovateľmi stavu senzora by mohli byť „zašumenosť“ meraného priebehu glukózy zo senzora a teda „zašumenosť“ ISIG signálu a zároveň samotná veľkosť ISIG signálu. Ukážme na dátach od jedného subjektu. Počas posledných zhruba dvoch mesiacov subjekt použil 5 snezorov.
Senzor 1.
Prvý senzor bol zavedený jedného dňa večer a používaný počas nasledujúcich 7 dní. Namerané CGM dáta sú na nasledujúcom obrázku.
Počas dňa 1., dňa 2. a dňa 3. je meranie v poriadku. Kalibrácia je v rámci možností úspešná a glukóza zo senzora súhlasí s hodnotou z glukomera. Signál ISIG sa mení v dostatočne veľkom intervale a jeho priebeh je hladký, nie je zašumený.
V deň 4. po obede začína hodnota signálu ISIG klesať. Dôvodom zjavne nie je pokles koncentrácie glukózy. Glykémia ráno v deň 3. a glykémia ráno v deň 4. je prakticky rovnaká ale veľkosť signálu ISIG je podstatne rozdielna. Navyše v deň 5. sa signál ISIG stáva zašumeným. Sú v ňom čo do veľkosti malé avšak rýchle a časté zmeny - teda šum. Pritom priemerná hodnota signálu ISIG je prakticky konštantná a to nie len v dni 5. ale aj v dňoch 6. a 7. Toto je jednoznačným znakom, že daný senzor už nemeria spoľahlivo. V tomto prípade teda bola životnosť senzora zhruba 3,5 dňa. Zvyšné meranie je nespoľahlivé, prakticky nepoužiteľné.
Šum ISIGu sa samozrejme prejaví aj na v reálnom čase zobrazovanej glukóze zo senzora. Ak je glukóza zo senzora zašumená v porovnaní napríklad s prvými dňami používania senzora, tak je to známka, že so senzorom sa pravdepodobne niečo stalo a nemeria spoľahlivo.
Druhým ukazovateľom opotrebovanosti senzora by mohol byť pomer hodnoty glykémie nameranej glukomerom (označme $BG$) k hodnote signálu $ISIG$ v tom istom čase, teda
$$
\text{kontrolný pomer} = \frac{BG}{ISIG} \qquad \left[ \frac{\text{mmol/l}}{\text{nA}} \right]
$$
Počas dňa 1., dňa 2. a dňa 3. je meranie v poriadku. Kalibrácia je v rámci možností úspešná a glukóza zo senzora súhlasí s hodnotou z glukomera. Signál ISIG sa mení v dostatočne veľkom intervale a jeho priebeh je hladký, nie je zašumený.
V deň 4. po obede začína hodnota signálu ISIG klesať. Dôvodom zjavne nie je pokles koncentrácie glukózy. Glykémia ráno v deň 3. a glykémia ráno v deň 4. je prakticky rovnaká ale veľkosť signálu ISIG je podstatne rozdielna. Navyše v deň 5. sa signál ISIG stáva zašumeným. Sú v ňom čo do veľkosti malé avšak rýchle a časté zmeny - teda šum. Pritom priemerná hodnota signálu ISIG je prakticky konštantná a to nie len v dni 5. ale aj v dňoch 6. a 7. Toto je jednoznačným znakom, že daný senzor už nemeria spoľahlivo. V tomto prípade teda bola životnosť senzora zhruba 3,5 dňa. Zvyšné meranie je nespoľahlivé, prakticky nepoužiteľné.
Šum ISIGu sa samozrejme prejaví aj na v reálnom čase zobrazovanej glukóze zo senzora. Ak je glukóza zo senzora zašumená v porovnaní napríklad s prvými dňami používania senzora, tak je to známka, že so senzorom sa pravdepodobne niečo stalo a nemeria spoľahlivo.
Druhým ukazovateľom opotrebovanosti senzora by mohol byť pomer hodnoty glykémie nameranej glukomerom (označme $BG$) k hodnote signálu $ISIG$ v tom istom čase, teda
$$
\text{kontrolný pomer} = \frac{BG}{ISIG} \qquad \left[ \frac{\text{mmol/l}}{\text{nA}} \right]
$$
Ak je tento pomer relatívne konštantný počas určitého obdobia, tak počas tohto obdobia senzor meria spoľahlivo a stále rovnako. Aspoň teoreticky.
Vyhodnoťme tento „kontrolný pomer“ pre prvé ranné meranie glykémie v každom dni. Toto meranie je vyznačené na obrázku vyššie spolu s príslušnou hodnotou $ISIG$. Hodnoty sú v nasledujúcej tabuľke:
Počas prvých štyroch dní sa pri prvom rannom meraní udržiava zhruba konštantná hodnota pomeru $BG/ISIG$ (priemer prvých štyroch dní je 0,286 [mmol/l/nA]). Vo zvyšných dňoch sa hodnota $BG/ISIG$ vzhľadom na prvé štyri dni zvyšuje. To preto, že $ISIG$ klesol ale nie preto, že by klesli ranné glykémie. Zmena pomeru $BG/ISIG$ je teda známkou nespoľahlivo merajúceho senzora.
Vyhodnoťme tento „kontrolný pomer“ pre prvé ranné meranie glykémie v každom dni. Toto meranie je vyznačené na obrázku vyššie spolu s príslušnou hodnotou $ISIG$. Hodnoty sú v nasledujúcej tabuľke:
| deň | $BG$ [mmol/l] | $ISIG$ [nA] | $BG/ISIG$ [mmol/l/nA] |
| 1 | 10.2 | 32.52 | 0.31 |
| 2 | 7.8 | 27.70 | 0.28 |
| 3 | 7.3 | 30.62 | 0.24 |
| 4 | 9.5 | 30.72 | 0.31 |
| 5 | 7.7 | 18.06 | 0.42 |
| 6 | 10.1 | 18.28 | 0.55 |
| 7 | 10.9 | 16.74 | 0.65 |
Počas prvých štyroch dní sa pri prvom rannom meraní udržiava zhruba konštantná hodnota pomeru $BG/ISIG$ (priemer prvých štyroch dní je 0,286 [mmol/l/nA]). Vo zvyšných dňoch sa hodnota $BG/ISIG$ vzhľadom na prvé štyri dni zvyšuje. To preto, že $ISIG$ klesol ale nie preto, že by klesli ranné glykémie. Zmena pomeru $BG/ISIG$ je teda známkou nespoľahlivo merajúceho senzora.
Senzor 2.
Pozrime sa na druhý senzor. Bol zavedený po obede a používaný nasledujúcich 5 dní, ktoré sú na nasledujúcom obrázku:
Opäť je zreteľný rozdiel medzi veľkosťou šumu signálu ISIG počas prvých dvoch dní a počas zvyšných dní.
Senzor 3.
Tretí senzor je asi výnimka potvrdzujúca pravidlo. Bol zavedený večer a používaný nasledujúcich 7 dní. Dáta sú na nasledujúcom obrázku:
Žiadny šum. Senzor meral spoľahlivo po celý čas. Pomer $BG/ISIG$ sa však neustále trochu menil. To je normálne. Práve preto je potrebná kalibrácia.
Mimochodom tieto grafy sú nakreslené tak, že keď sa na grafe prekrýva hodnota glykémie s hodnotou ISIG, tak pomer $BG/ISIG$ je práve 0,25 [mmol/l/nA] (alebo 4.5 [mg/ml/nA]). V tomto konkrétnom prípade, teda pre tento konkrétny subjekt je možné usúdiť, že ak senzor funguje správne, tak pomer $BG/ISIG$ sa väčšinu času udržiava blízko hodnoty 0,25 [mmol/l/nA].
Mimochodom tieto grafy sú nakreslené tak, že keď sa na grafe prekrýva hodnota glykémie s hodnotou ISIG, tak pomer $BG/ISIG$ je práve 0,25 [mmol/l/nA] (alebo 4.5 [mg/ml/nA]). V tomto konkrétnom prípade, teda pre tento konkrétny subjekt je možné usúdiť, že ak senzor funguje správne, tak pomer $BG/ISIG$ sa väčšinu času udržiava blízko hodnoty 0,25 [mmol/l/nA].
Senzor 4.
Štvrtý senzor bol zavedený večer a používaný nasledujúcich 6 dní - dáta na nasledujúcom obrázku:
S narastajúcim časom používania je možné sledovať nárast šumu. Zmeny pomeru $BG/ISIG$ pri tomto konkrétnom senzore nie sú také zrejmé a jednoznačné ako pri prvom uvedenom senzore. V posledných dvoch dňoch je však pomer $BG/ISIG$ väčšinu času iný (takto od oka) ako v predchádzajúcich dňoch. V tabuľke sú uvedené a v grafe vyznačené body pre porovnanie pomeru $BG/ISIG$ v jednotlivých dňoch:
| deň | BG [mmol/l] | ISIG [nA] | BG/ISIG [mmol/l/nA] |
| 1 | 7.88 | 31.88 | 0.25 |
| 2 | 7.72 | 36.16 | 0.21 |
| 3 | 7.99 | 25.28 | 0.32 |
| 4 | 13.6 | 52.54 | 0.26 |
| 5 | 8.6 | 30.18 | 0.28 |
| 6 | 11.55 | 28.82 | 0.40 |
Senzor 5.
Piaty senzor je opäť jasnou ukážkou zhoršovania kvality merania s postupom času používania senzora. Narastá šum, mení sa aj pomer $BG/ISIG$. Viď nasledujúci graf a tabuľku (body z tabuľky vyznačené v grafe).
| deň | BG [mmol/l] | ISIG [nA] | BG/ISIG [mmol/l/nA] |
| 1 | 4.66 | 15.7 | 0.30 |
| 2 | 11.21 | 48.12 | 0.23 |
| 3 | 11.43 | 49.4 | 0.23 |
| 4 | 12.04 | 51.3 | 0.23 |
| 5 | 8.27 | 23.14 | 0.36 |
| 6 | 6.99 | 17.74 | 0.39 |
| 7 | 13.1 | 12.46 | 1.05 |
MT
p.s. Tie 7 dňové obrázky majú dlhšiu stranu dlhú „až“ 1680 pixelov, a hnusoba google mi ich skomprimoval - jednoducho nedovolí dať neskomprimované :( Ospravedlňte preto prosím zníženú kvalitu.
p.s. Tie 7 dňové obrázky majú dlhšiu stranu dlhú „až“ 1680 pixelov, a hnusoba google mi ich skomprimoval - jednoducho nedovolí dať neskomprimované :( Ospravedlňte preto prosím zníženú kvalitu.
22. 11. 2014
7. 11. 2014
25. 10. 2014
Poznámky k záverečnej správe projektu DiaDAQ
Autorský tím projektu DiaDAQ (Diabetic Data Acquisition) predložil žiadosť o podporu projektu 14. novembra 2013, v deň, ktorý je svetovým dňom diabetu. Členmi tímu sú študentka, študenti a výskumný pracovník, ktorí sa v rámci svojho štúdia a práce venujú Biokybernetike a jej aplikácii v oblasti riadenia a modelovania diabetu.
Autorský tím študuje a pracuje na FEI STU v Bratislave:
Autorský tím študuje a pracuje na FEI STU v Bratislave:
- Marián Tárník
Výskumný pracovník ÚRK FEI STU. - Ivan Ottinger
Doktorand, odbor Kybernetika.
Dizertačná práca zameraná na algoritmy riadenia dávkovania inzulínu. - Tomáš Ludwig
Doktorand, odbor Kybernetika.
Dizertačná práca zameraná na modelovanie a predikciu vývoja glykémie v čase. - Katarína Gubánová
Študentka inžinierskeho štúdia, odbor Kybernetika.
Téma diplomovej práce: Simulačné experimenty pre vzdelávanie diabetikov. - Matúš Rebro
Študent inžinierskeho štúdia, odbor Kybernetika.
Téma diplomovej práce: Automatizované dávkovanie inzulínu.
Nadácia Tatra banky podporila projekt sumou 2400 EUR v rámci grantového programu E-Talent. Tieto finančné prostriedky boli použité na nákup technických prostriedkov potrebných pre riešenie úloh projektu. Nákup bol realizovaný vo februári 2014. Rozpis položiek:
- Guardian REAL-Time systém - jedna sada, obsahuje glukózový monitor, vysielač MiniLink a ostatné príslušenstvo.
- Enlite senzor - spolu 32 kusov.
- Glukomer FreeStyle Optium - dve súpravy.
- Testovacie prúžky - päť balení, balenie po 50 prúžkov.
Cieľom projektu DiaDAQ bolo získanie a spracovanie dát potrebných pre aplikácie Biokybernetiky v oblasti liečby ochorenia diabetes mellitus 1. typu. V pláne bolo získať dáta od rôznych subjektov, pričom subjektom nazývame osobu s diabetom. Spolu 32 kusov senzorov využiteľných v nasledujúcich piatich mesiacoch umožňovalo rôzne alternatívy harmonogramu spolupráce so subjektmi. Zároveň bol k dispozícii dostatočný čas pre hľadanie subjektov.
V marci a v apríli nám Subjekt s veľkým S poskytol namerané dáta. Využilo sa 8 senzorov. V tomto prípade mal Subjekt k dispozícii vysielač MiniLink z inej predchádzajúcej spolupráce a k tomu vlastnú inzulínovú pumpu. Od konca marca do začiatku mája sme vďaka členke autorského tímu nadviazali spoluprácu so subjektom č. 2. Pri tejto spolupráci sa využilo celkom 8 senzorov a subjekt využíval kompletný systém pre kontinuálne monitorovanie glykémie zakúpený pre projekt DiaDAQ. Začiatkom apríla sne sa obrátili na občianske združenie diabetikinfo.sk s prosbou o sprostredkovanie spolupráce s ďalšími subjektmi. O. z. diabetikinfo.sk sprostredkovalo v rámci projektu DiaDAQ spoluprácu s ďalšími tromi subjektmi (subjekt č. 3 až 5). Celkovo sa v mesiacoch apríl až jún využilo 16 senzorov.
Hlavným výsledkom projektu DiaDAQ sú rozličné sady dát. Každý subjekt poskytol jednu sadu dát. Zoznam subjektov:
Jednotlivé sady dát pozostávajú spravidla z niekoľkých tabuliek, dátových súborov a grafov. Zdrojom tabuliek je softvér dodávaný k systému kontinuálneho monitorovania glykémie, ktorý umožňuje prenos dát zo zariadenia, ich zobrazenie a export. Niektoré tabuľky však boli zapisované manuálne ako štandardný diabetický denník.
Boli vytvorené nástroje pre spracovanie danej sady dát. Príkladom spracovania je napr. denný sumár, ktorý zlúči dáta z jedného dňa z rôznych tabuliek (manuálne zapisovaných a vyexportovaných z originálneho softvéru). K dispozícii sú tak dáta v jednotnom formáte a ich grafické zobrazenie. Uľahčuje to výber dát pre ďalšiu prácu.
Príkladom ďalšej práce s dátami je identifikácia matematického modelu, ktorý vystihuje priebeh glykémie v danej situácii. Spracované dáta sú v tomto období využívané v rámci diplomových a dizertačných prác členov autorského tímu.
Samotné dáta a skúsenosti nadobudnuté pri ich získavaní je možné využiť pri vzdelávaní ľudí s diabetom a ich blízkych. Jeden denný sumár (prípadne iný report) je výhodnejší ako niekoľko reportov z rôznych zdrojov. Uľahčuje to prehľad vo všetkých dostupných záznamoch súvisiacich s diabetom. Človek s diabetom sa tak môže poučiť z týchto záznamov. Nástroje pre zlúčenie dát z rôznych zdrojov tak prispievajú k vzdelávaniu doabetikov.
Simulácie môžu slúžiť ako podporný nástroj napr. pri vysvetľovaní princípov inzulínovej liečby. Je možné nasimulovať rôzne scenáre zodpovedajúce očakávanému priebehu glykémie a demonštrovať tak súvislosti medzi jednotlivými veličinami. Základom simulácii sú matematické modely a tie sú vytvárané s využitím dát, takých, ktoré boli zozbierané v rámci projektu DiaDAQ.
V priebehu spolupráce s o. z. diabetikinfo.sk bol záujem aj o informácie o princípe merania koncentrácie glukózy v podkoží a iné informácie technického charakteru týkajúce sa „senzora“, teda systému pre kontinuálne monitorovanie glykémie. Zúčastnili sme sa rekondičného pobytu organizovaného o. z. diabetikinfo.sk a svojou malou troškou sme prispeli do diskusie o senzoroch a kontinuálnom monitoringu. Prikladáme pár fotografií z rekondičného pobytu:
| č.s. | Počet senzorov | Poznámka | |
| s.č.1 | Subjekt | 8 | Paradigm Veo, MiniLink, dia denník. |
| s.č.2 | Slovníček | 8 | Accu-Check Spirit Combo, Guardian monitor, MiniLink, dia denník. |
| s.č.3 | Kvetinka | 5 | Inzulínové perá, Guardian monitor, MiniLink, dia denník. |
| s.č.4 | diabetikinfo | 5 | Paradigm Veo, MiniLink, Bolus Wizard. |
| s.č.5 | Nairo | 6 | Paradigm Veo, MiniLink, Bolus Wizard. |
Jednotlivé sady dát pozostávajú spravidla z niekoľkých tabuliek, dátových súborov a grafov. Zdrojom tabuliek je softvér dodávaný k systému kontinuálneho monitorovania glykémie, ktorý umožňuje prenos dát zo zariadenia, ich zobrazenie a export. Niektoré tabuľky však boli zapisované manuálne ako štandardný diabetický denník.
Boli vytvorené nástroje pre spracovanie danej sady dát. Príkladom spracovania je napr. denný sumár, ktorý zlúči dáta z jedného dňa z rôznych tabuliek (manuálne zapisovaných a vyexportovaných z originálneho softvéru). K dispozícii sú tak dáta v jednotnom formáte a ich grafické zobrazenie. Uľahčuje to výber dát pre ďalšiu prácu.
Príkladom ďalšej práce s dátami je identifikácia matematického modelu, ktorý vystihuje priebeh glykémie v danej situácii. Spracované dáta sú v tomto období využívané v rámci diplomových a dizertačných prác členov autorského tímu.
Samotné dáta a skúsenosti nadobudnuté pri ich získavaní je možné využiť pri vzdelávaní ľudí s diabetom a ich blízkych. Jeden denný sumár (prípadne iný report) je výhodnejší ako niekoľko reportov z rôznych zdrojov. Uľahčuje to prehľad vo všetkých dostupných záznamoch súvisiacich s diabetom. Človek s diabetom sa tak môže poučiť z týchto záznamov. Nástroje pre zlúčenie dát z rôznych zdrojov tak prispievajú k vzdelávaniu doabetikov.
Simulácie môžu slúžiť ako podporný nástroj napr. pri vysvetľovaní princípov inzulínovej liečby. Je možné nasimulovať rôzne scenáre zodpovedajúce očakávanému priebehu glykémie a demonštrovať tak súvislosti medzi jednotlivými veličinami. Základom simulácii sú matematické modely a tie sú vytvárané s využitím dát, takých, ktoré boli zozbierané v rámci projektu DiaDAQ.
V priebehu spolupráce s o. z. diabetikinfo.sk bol záujem aj o informácie o princípe merania koncentrácie glukózy v podkoží a iné informácie technického charakteru týkajúce sa „senzora“, teda systému pre kontinuálne monitorovanie glykémie. Zúčastnili sme sa rekondičného pobytu organizovaného o. z. diabetikinfo.sk a svojou malou troškou sme prispeli do diskusie o senzoroch a kontinuálnom monitoringu. Prikladáme pár fotografií z rekondičného pobytu:
5. 10. 2014
Príklad výsledku identifikácie
Nasledujúce slúži len ako ilustrácia výsledku identifikácie modelu („biokybernetického“), ktorý vystihuje priebeh glykémie v danej situácii. Výsledok je prezentovaný len graficky. Podrobnosti sú vynechané, hádam sa k nim dostaneme neskôr.
Majme dáta z obdobia raňajok z dvoch dní. V deň prvý boli raňajky o 9:07. Dáta pre časový interval 30 minút pred a 108 minút po raňajkách vyzerajú nasledovne:
Na raňajky bolo 45 gramov sacharidov, bolus 3,7 U. V čase 10:15 bolo ďalšie jedlo, asi desiata, ale táto skutočnosť je pri identifikácii modelu v tomto prípade zanedbaná (akokoľvek čudne to znie). V deň druhý boli raňajky o 9:22. Opäť, dáta pre ten istý interval v okolí raňajok vyzerajú nasledovne:
Pre vystihnutie priebehu glykémie z oboch dní uvažujme priemer (v tomto bode zanedbáme tú „desiatu“). Priemerné hodnoty sacharidov, bolusov a priemerný priebeh glykémie sú nasledovné:
Cieľom identifikácie je aby výstup modelu vystihoval priebeh nameranej glykémie. Model bol identifikovaný s využitím priemerných hodnôt. Je to spôsob ako zohľadniť vplyv oboch dní. Výsledok identifikácie je na nasledujúcom obrázku porovnaný s priemerným priebehom glykémie:
Ak napríklad budú vstupom do modelu sacharidy a bolus z dňa prvého, potom porovnanie výstupu modelu a nameraného priebehu glykémie vyzerá nasledovne:
MT
Majme dáta z obdobia raňajok z dvoch dní. V deň prvý boli raňajky o 9:07. Dáta pre časový interval 30 minút pred a 108 minút po raňajkách vyzerajú nasledovne:
Na raňajky bolo 45 gramov sacharidov, bolus 3,7 U. V čase 10:15 bolo ďalšie jedlo, asi desiata, ale táto skutočnosť je pri identifikácii modelu v tomto prípade zanedbaná (akokoľvek čudne to znie). V deň druhý boli raňajky o 9:22. Opäť, dáta pre ten istý interval v okolí raňajok vyzerajú nasledovne:
Pre vystihnutie priebehu glykémie z oboch dní uvažujme priemer (v tomto bode zanedbáme tú „desiatu“). Priemerné hodnoty sacharidov, bolusov a priemerný priebeh glykémie sú nasledovné:
Cieľom identifikácie je aby výstup modelu vystihoval priebeh nameranej glykémie. Model bol identifikovaný s využitím priemerných hodnôt. Je to spôsob ako zohľadniť vplyv oboch dní. Výsledok identifikácie je na nasledujúcom obrázku porovnaný s priemerným priebehom glykémie:
Ak napríklad budú vstupom do modelu sacharidy a bolus z dňa prvého, potom porovnanie výstupu modelu a nameraného priebehu glykémie vyzerá nasledovne:
MT
3. 10. 2014
Krivka aktívneho inzulínu
Bolus wizard je nástroj, pomocou ktorého je možné priamo v pumpe (Medtronic) vypočítať bolus. Bolus wizard pri výpočte bolusu vyhodnocuje aj tzv. aktívny inzulín - inzulín, ktorý ešte účinkuje od posledného bolusu, zostatkový inzulín, „insulin on board“...
Pre výpočet aktívneho inzulínu sa používa krivka aktívneho inzulínu. Dáva do vzťahu čas od podania bolusu a množstvo inzulínu, ktoré akoby ostáva, ktorého účinok sa ešte prejaví.
Narýchlo vygooglené letáky hovoria o krivke aktívneho inzulínu nasledovné:
Krivka vyzerá nasledovne:
Manuál pumpy Paradigm 522 obsahuje aspoň trošku lepší obrázok krivky aktívneho inzulínu:
Manuál odkazuje na článok autorov Mudalair a kol., ktorý už poznáme zo štúdia farmakodynamiky. Údajne graf krivky v manuály je adaptáciou z uvedeného článku. Žiadny podobný graf sa pritom v článku nenachádza. Viem si však zhruba predstaviť čo vyjadruje krivka aktívneho inzulínu vo vzťahu k farmakodynamike inzulínu prezentovanej v uvedenom článku.
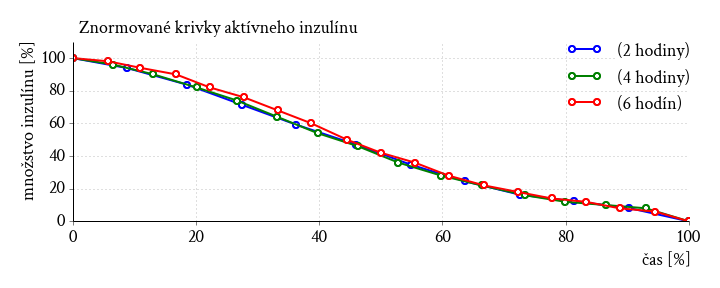
Krivku aktívneho inzulínu je možné aj odmerať. Myslím tým jednoducho sledovať údaj „aktívny inzulín“ v pumpe po boluse. „Meral“ som nasledovne. Manuálne (nie pomocou bolus wizardu) som podal bolus 5 U. Potom som v pravidelných intervaloch „otvoril“ bolus wizard, pozrel hodnotu údaja aktívny inzulín a zapísal spolu s časom. Odmeral som krivku pre jej tri rôzne nastavenia - dĺžky účinku inzulínu. Konkrétne „active insulin time“ 2 hod., 4 hod. a 6 hod (8 hodín sa mi nechcelo čakať). Meranie prebehlo na pumpe Paradigm 522 (pre mňa veľmi vzácnej). Starší typ ale novšie pumpy sú myslím v tomto také isté. Nie, pumpa počas „merania“ nebola k nikomu pripojená.
Namerané krivky sú na nasledujúcom obrázku. 100 % množstva inzulínu je v tomto prípade 5 U.
Jednoznačne sa to podobá na to čo je uvedené v manuáli. Ak znormujeme čas všetkých nameraných kriviek na 0 až 100 % vidíme, že tie krivky sú rovnaké čo sa tvaru týka:
Z tvaru krivky sa dá usúdiť, že matematickým predpisom, ktorý vystihuje krivku by mohla byť polynomiálna funkcia s polynómom 3. stupňa.
$$
\begin{align*}
y &= f(x) \\
y &= p_3 x^3 + p_2 x^2 + p_1 x + p_0
\end{align*}
$$
Podľa obrázku vyššie môžme celkom logicky žiadať aby $100 = f(0)$, $50=f(50)$ a $0 = f(100)$. Z toho nie práve očividne, ale predsa vyplýva, že pomyselná ideálna krivka môže byť daná parametrami $p_3=2e-4$, $p_2=-3e-2$, $p_1 = -9e-4$ a $p_0 = 100$ (pre analytické odvodenie by sme uvažovali aj požiadavky na deriváciu $f'(x)$ atď.), teda:
$$
f_{ideal}(x) = 0.0002 x^3 - 0.003 x^2 - 0.0009 x + 100
$$
Parametre modelu krivky je samozrejme možné získať aj v zmysle metódy najmenších štvorcov (regresnou analýzou). Výsledkom je
$$
f_{model}(x) =1.26 \cdot 10^{-4} x^3 -1.495\cdot 10^{-4} x^2 -7.46\cdot 10^{-4}x + 101.81
$$
Graficky sú tieto funkcie porovnané s nameranými dátami na nasledujúcom obrázku. Samozrejme „model“ lepšie vystihuje namerané dáta ako vymyslená ideálna krivka.
Majúc aproximáciu krivky aktívneho inzulínu, všeličo by sa dalo robiť. Možno niekedy nabudúce.
MT
p.s. Tento krát je font pre text v grafoch zavedený konečne inteligentne... Stačilo súbor fontu dať medzi ostatné fonty matplolib-u (to som mal aj pred tým) a potom vymazať súbor ~/.matplotlib/fontlist.cache. Následne po importe matplotlib-u si tento všimne, že tam ten súbor chýba a vyrobí nový. Nový súbor už obsahoval aj info o novom fonte, pretože ho našiel v adresári. Konečne stačilo štandardne zmeniť rc parameter font.family a veselo používať nový font.
30. 9. 2014
Farmakokinetika a farmakodynamika inzulínu - časť 3.
Podľa Bergmanovho minimálneho modelu (BMM) [1, 2] je možné opísať inzulín-glukózový systém nasledovne. Z istého pohľadu (minimálne môjho) vstupmi modelu sú koncentrácia inzulínu v krvi $I(t)$ [$\mu$U/ml] a niečo čo teraz nazvem rýchlosť „objavovania sa“ glukózy v krvi $Ra(t)$ [mg/kg/min].
Ten názov je prekladom anglického Glucose Rate of Appearance. Preto $Ra(t)$. Glukóza sa v krvi môže „objavovať“ po tom čo niečo zjeme alebo ak je glukóza podaná priamo „do žily“. V druhom prípade môžme $Ra(t)$ nazvať aj rýchlosť podávania glukózy („do žily“, nie ako rýchlo nosia koláče na stôl). Vstup $Ra(t)$ sa v „štandardnom“ minimálnom modely nenachádza priamo. Je skrytý v začiatočnom stave zodpovedajúcej diferenciálnej rovnice.
Model je daný v tvare $$ \begin{align}
\dot X(t) &= - p_2 X(t) + p_2 S_I \left( I(t) - I_b \right) & & X(0) = 0 \\
\dot G(t) &= - \left( S_G + X(t) \right) G(t) + S_G G_b + \left( \frac{1}{V} \right) Ra(t) & & G(0) = G_b \label{rovnica}
\end{align}$$ kde $G(t)$ [mg/dl] je koncentrácia glukózy v krvi, $S_G$ [1/min] je parameter, ktorý udáva ako rýchlo sa glukóza stráca „sama od seba“, $S_I$ [ml/$\mu$U/min] sa označuje ako index citlivosti na inzulín a $p_2$ [1/min] je ďalší parameter. $I_b$ [$\mu$U/ml] a $G_b$ [mg/dl] sú bazálne hodnoty koncentrácií inzulínu a glukózy v uvedenom poradí. $V$ [dl/kg] je objem, do ktorého sa dostáva glukóza, vztiahnutý na jeden kilogram telesnej hmotnosti $BW$ [kg]. Signál $X(t)$ sa označuje ako „remote insulin“. Nech už to znamená čokoľvek, táto premenlivá časová konštanta vyjadruje vplyv inzulínu na „strácanie sa“ glukózy.
Signál $X(t)$ závisí od koncentrácie inzulínu $I(t)$. Model vstrebávania inzulínu (MVI), ktorého výstupom je $I(t)$ sme uviedli v predchádzajúcej časti. Spojením MVI a BMM dostávame celok. Schematicky:
Vstupmi sú rýchlosť podávania inzulínu $v(t)$ a rýchlosť podávania glukózy $Ra(t)$.
Farmakodynamika (FD) je doslova rýchlosť podávania (prísunu, viď časť 1.) glukózy do krvi. V modeli je to teda signál $Ra(t)$. V tomto prípade získame signál $Ra(t)$ tak, že lineárne interpolujeme pôvodné FD dáta a predelíme ich hodnotou hmotnosti subjektu $BW = 75$ [kg].
Ak model nastavíme tak aby zodpovedal naperanej farmakokinetike a zároveň farmakodynamike, potom výstupom modelu musí byť prakticky konštantná glykémia - taký je princíp merania farmakodynamiky.
Pre danú farmakokinetiku (FK) závisia FD vlastnosti modelu výlučne od parametrov BMM časti modelu. MVI už máme nastavený tak, že zodpovedá FK. Ostáva BMM. Rovnicu $\eqref{rovnica}$ je možné napísať v tvare $$ \begin{align}
\dot G(t) &= - S_G G(t) + S_G G_b + \frac{1}{V} \left( Ra(t) - V \cdot X(t) \cdot G(t) \right)
\end{align}$$ Je teda zrejmé, že $G(t)$ zostane konštantné ak $Ra(t) = V \cdot X(t) \cdot G(t)$. Ak $Ra(t)$ je rýchlosť prísunu, tak výraz $V \cdot X(t) \cdot G(t)$ je vlastne rýchlosť „odsunu“ glukózy vplyvom inzulínu. Modelovanie farmakodynamiky teda závisí hlavne od priebehu signálu $X(t)$.
Z pohľadu modelovania FD je cieľom aby $G(t)$ bol po celý čas čo najbližšie k ustálenej hodnote $G_b$. To závisí samozrejme od všetkých parametrov BMM časti modelu (a to ešte MVI časť je zafixovaná). Tým sa stáva hľadanie parametrov BMM časti náročnejšie, atď... Opäť, pretože som lenivý, tak v tomto prípade som parametre BMM odhadol, „kvalifikovane“, na základe parametrov uvedených v [2]. Konkrétne:
$$ \begin{align*}
p_2 &= 0,0144 \text{[1/min]} \\
S_I &= 0,00127545 \text{[ml/$\mu$U/min]} \\
S_G &=0.014 \text{[1/min]} \\
G_b &=100 \text{[mg/dl]} \\
V &= 1,7 \text{[dl/mg]}
\end{align*}$$ Výsledok simulácie je na nasledujúcom obrázku:

Glukóza sa udržiava zhruba v hodnotách $G_b \pm 10\%$, teda je prakticky konštantná. Čo sa stane ak $Ra(t) = 0$? Simulujme:

Nech hranica hypoglykémie je 3,5 mmol/l. Výsledkom simulácie je život ohrozujúce hypo - podľa očakávania.
MT
Ten názov je prekladom anglického Glucose Rate of Appearance. Preto $Ra(t)$. Glukóza sa v krvi môže „objavovať“ po tom čo niečo zjeme alebo ak je glukóza podaná priamo „do žily“. V druhom prípade môžme $Ra(t)$ nazvať aj rýchlosť podávania glukózy („do žily“, nie ako rýchlo nosia koláče na stôl). Vstup $Ra(t)$ sa v „štandardnom“ minimálnom modely nenachádza priamo. Je skrytý v začiatočnom stave zodpovedajúcej diferenciálnej rovnice.
\dot X(t) &= - p_2 X(t) + p_2 S_I \left( I(t) - I_b \right) & & X(0) = 0 \\
\dot G(t) &= - \left( S_G + X(t) \right) G(t) + S_G G_b + \left( \frac{1}{V} \right) Ra(t) & & G(0) = G_b \label{rovnica}
\end{align}$$ kde $G(t)$ [mg/dl] je koncentrácia glukózy v krvi, $S_G$ [1/min] je parameter, ktorý udáva ako rýchlo sa glukóza stráca „sama od seba“, $S_I$ [ml/$\mu$U/min] sa označuje ako index citlivosti na inzulín a $p_2$ [1/min] je ďalší parameter. $I_b$ [$\mu$U/ml] a $G_b$ [mg/dl] sú bazálne hodnoty koncentrácií inzulínu a glukózy v uvedenom poradí. $V$ [dl/kg] je objem, do ktorého sa dostáva glukóza, vztiahnutý na jeden kilogram telesnej hmotnosti $BW$ [kg]. Signál $X(t)$ sa označuje ako „remote insulin“. Nech už to znamená čokoľvek, táto premenlivá časová konštanta vyjadruje vplyv inzulínu na „strácanie sa“ glukózy.
Signál $X(t)$ závisí od koncentrácie inzulínu $I(t)$. Model vstrebávania inzulínu (MVI), ktorého výstupom je $I(t)$ sme uviedli v predchádzajúcej časti. Spojením MVI a BMM dostávame celok. Schematicky:
Vstupmi sú rýchlosť podávania inzulínu $v(t)$ a rýchlosť podávania glukózy $Ra(t)$.
Farmakodynamika (FD) je doslova rýchlosť podávania (prísunu, viď časť 1.) glukózy do krvi. V modeli je to teda signál $Ra(t)$. V tomto prípade získame signál $Ra(t)$ tak, že lineárne interpolujeme pôvodné FD dáta a predelíme ich hodnotou hmotnosti subjektu $BW = 75$ [kg].
Ak model nastavíme tak aby zodpovedal naperanej farmakokinetike a zároveň farmakodynamike, potom výstupom modelu musí byť prakticky konštantná glykémia - taký je princíp merania farmakodynamiky.
Pre danú farmakokinetiku (FK) závisia FD vlastnosti modelu výlučne od parametrov BMM časti modelu. MVI už máme nastavený tak, že zodpovedá FK. Ostáva BMM. Rovnicu $\eqref{rovnica}$ je možné napísať v tvare $$ \begin{align}
\dot G(t) &= - S_G G(t) + S_G G_b + \frac{1}{V} \left( Ra(t) - V \cdot X(t) \cdot G(t) \right)
\end{align}$$ Je teda zrejmé, že $G(t)$ zostane konštantné ak $Ra(t) = V \cdot X(t) \cdot G(t)$. Ak $Ra(t)$ je rýchlosť prísunu, tak výraz $V \cdot X(t) \cdot G(t)$ je vlastne rýchlosť „odsunu“ glukózy vplyvom inzulínu. Modelovanie farmakodynamiky teda závisí hlavne od priebehu signálu $X(t)$.
Z pohľadu modelovania FD je cieľom aby $G(t)$ bol po celý čas čo najbližšie k ustálenej hodnote $G_b$. To závisí samozrejme od všetkých parametrov BMM časti modelu (a to ešte MVI časť je zafixovaná). Tým sa stáva hľadanie parametrov BMM časti náročnejšie, atď... Opäť, pretože som lenivý, tak v tomto prípade som parametre BMM odhadol, „kvalifikovane“, na základe parametrov uvedených v [2]. Konkrétne:
$$ \begin{align*}
p_2 &= 0,0144 \text{[1/min]} \\
S_I &= 0,00127545 \text{[ml/$\mu$U/min]} \\
S_G &=0.014 \text{[1/min]} \\
G_b &=100 \text{[mg/dl]} \\
V &= 1,7 \text{[dl/mg]}
\end{align*}$$ Výsledok simulácie je na nasledujúcom obrázku:

Glukóza sa udržiava zhruba v hodnotách $G_b \pm 10\%$, teda je prakticky konštantná. Čo sa stane ak $Ra(t) = 0$? Simulujme:

Nech hranica hypoglykémie je 3,5 mmol/l. Výsledkom simulácie je život ohrozujúce hypo - podľa očakávania.
Referencie
| [1] | Natal van Riel. Minimal Models for Glucose and Insulin Kinetics - a Matlab implementation. Eindhoven University of Technology. |
| [2] | Pau Herrero, Pantelis Georgiou, Nick Oliver, Monika Reddy, Desmond Johnston, Christofer Toumazou. A composite model of glucagon-glucose dynamics for in silico testing of bihormonal glucose controllers. Journal of Diabetes Science and Technology, July 2013, Volume 7, Issue 4: pages 941-951 |
MT
7. 6. 2014
Weekend Reading
Short Film
A children's guide to diabetes - short film from Fluent Studio on Vimeo (D-Mom Blog YouTube Tuesday).
MiniMed Duo
- New Medtronic Device Combines CGM Sensor & Insulin Infusion Site
- Feasibility of Adjacent Insulin Infusion and Continuous Glucose Monitoring via the Medtronic Combo-Set
- Press Release
Prakticky samé znamenia...
6. 6. 2014
Farmakokinetika a farmakodynamika inzulínu - časť 2.
Vynechajme asi milión detailov a najmä na základe [1] modelujme dynamiku vstrebávania do krvi podkožne podaného inzulínu nasledovne. Vstupom modelu je rýchlosť podávania inzulínu do podkožia $v(t)$ [$\mu$U/kg/min]. Výstupom modelu je koncentrácia inzulínu v krvi $I(t)$ [$\mu$U/ml].
Model je daný v tvare $$ \begin{align}
\dot S_1(t) &= - \left( \frac{1}{t_I} \right) S_1(t) + v(t) & & S_1(0) = S_{1b} \\
\dot S_2(t) &= - \left( \frac{1}{t_I} \right) S_2(t) + \left( \frac{1}{t_I} \right) S_1(t) & & S_2(0) = S_{2b} \\
\dot I(t) &= - k_I I(t) + \left( \frac{1}{t_I} \right) \left( \frac{1}{V_I} \right) S_2(t) & & I(0) = I_b
\end{align}$$ kde $S_1(t)$, $S_2(t)$ [$\mu$U/kg] sú ostatné stavové veličiny systému, $t_I$ [min] je časová konštanta vstrebávania, $V_I$ [dl/kg] je objem, do ktorého sa inzulín distribuuje na kg telesnej hmotnosti a $k_I$ [1/min] je rýchlosť prirodzeného strácania sa inzulínu. Index ${}_b$ značí bazálnu (ustálenú) hodnotu.
Koncentráciu inzulínu modelujeme v [$\mu$U/ml] a farmakokinetiku máme nameranú v [pmol/l]. Platí 1 U = 6000 pmol, preto 1/6 [$\mu$U/ml] = 1 [pmol/l], viď obrázok:

V opise merania farmakokinetiky v článku [2] sa píše, že dávka inzulínu bola 0,2 [U/kg]. Pre určenie absolútnej dávky inzulínu teda potrebujeme poznať hmotnosť subjektu. V článku [2] sa uvádza len, že subjekty boli muži a ich $\text{BMI} = 23,6 \pm 2,2$ [kg/m${}^2$]. Meranie prebehlo v USA a podľa Wikipedie má priemerný muž v USA výšku 1,763 m. Z toho vyplýva priemerná hmotnosť subjektov 73,35 kg. Zaokrúhlime to na $BW = 75$ [kg]. Celková dávka inzulínu teda je $0,2 \cdot 75 = 15$ [U] (t.j. 15 000 000 $\mu$U).
Pätnásť jednotiek je podaných hneď na začiatku merania farmakokinetiky a dávka je podaná v priebehu krátkeho času. Budeme uvažovať periódu vzorkovania $T_S = 5$ [min]. „Krátky čas“ je preto 5 minút. Vstup do modelu je v [$\mu$U/kg/min]. Po uvážení všetkého známeho vieme určiť rýchlosť podávania inzulínu takú, že za jednu periódu vzorkovania zodpovedá množstvu 15 U. Označme ju $v_{B}\delta(t) = \frac{15000000}{BW \cdot T_S} = 40000$ [$\mu$U/kg/min] (pričom signál $v_{B}\delta(t)$ na teraz „trvá“ jednu periódu vzorkovania).
V predchádzajúcej časti sme určili bazálnu koncentráciu inzulínu $I_b = 39$ [pmol/l] $= 6,5$ [$\mu$U/ml]. Pre ustálený (bazálny) stav modelu platí $$ \begin{align} S_{2b} &= \frac{k_I \cdot I_b}{ \frac{1}{t_I} \frac{1}{V_I} } \\
S_{1b} &= S_{2b} \\
v_b & = \frac{1}{t_I} S_{1b}
\end{align}$$ Bazálna koncentrácia inzulínu $I_b$ zodpovedá bazálnej rýchlosti podávania inzulínu $v_b = 110,838$ [$\mu$U/kg/min] čo je mimochodom 0,499 [U/h].
Celkový vstup do modelu potom je $v(t) = v_b + v_B \delta(t)$, kde $\delta(t)$ [1/min] je aproximácia Diracovho impulzu pre danú periódu vzorkovania pričom impulz začína v čase podania inzulínu a $v_B = 40000$ [$\mu$U/kg].
Úlohou je nájsť parametre modelu tak, aby sa výstup modelu zhodoval s nameranou farmakokinetikou. V tomto prípade som nepoužil žiadnu slušnú metódu pre hľadanie parametrov (pretože som lenivý, hanba mi) a „od oka“ som modifikoval pôvodné parametre v [1] (hovorme tomu kvalifikovaný odhad). Použité parametre
$$ \begin{align*} t_I &= 51,642 \text{[min]} \\
k_I &= 0,196 \text{[1/min]} \\
V_I &= 87 \text{[ml/kg]}
\end{align*}$$
Výsledok simulácie je na nasledujúcom obrázku:
Celkom dobre takto od oka...
MT
Model je daný v tvare $$ \begin{align}
\dot S_1(t) &= - \left( \frac{1}{t_I} \right) S_1(t) + v(t) & & S_1(0) = S_{1b} \\
\dot S_2(t) &= - \left( \frac{1}{t_I} \right) S_2(t) + \left( \frac{1}{t_I} \right) S_1(t) & & S_2(0) = S_{2b} \\
\dot I(t) &= - k_I I(t) + \left( \frac{1}{t_I} \right) \left( \frac{1}{V_I} \right) S_2(t) & & I(0) = I_b
\end{align}$$ kde $S_1(t)$, $S_2(t)$ [$\mu$U/kg] sú ostatné stavové veličiny systému, $t_I$ [min] je časová konštanta vstrebávania, $V_I$ [dl/kg] je objem, do ktorého sa inzulín distribuuje na kg telesnej hmotnosti a $k_I$ [1/min] je rýchlosť prirodzeného strácania sa inzulínu. Index ${}_b$ značí bazálnu (ustálenú) hodnotu.
Koncentráciu inzulínu modelujeme v [$\mu$U/ml] a farmakokinetiku máme nameranú v [pmol/l]. Platí 1 U = 6000 pmol, preto 1/6 [$\mu$U/ml] = 1 [pmol/l], viď obrázok:

V opise merania farmakokinetiky v článku [2] sa píše, že dávka inzulínu bola 0,2 [U/kg]. Pre určenie absolútnej dávky inzulínu teda potrebujeme poznať hmotnosť subjektu. V článku [2] sa uvádza len, že subjekty boli muži a ich $\text{BMI} = 23,6 \pm 2,2$ [kg/m${}^2$]. Meranie prebehlo v USA a podľa Wikipedie má priemerný muž v USA výšku 1,763 m. Z toho vyplýva priemerná hmotnosť subjektov 73,35 kg. Zaokrúhlime to na $BW = 75$ [kg]. Celková dávka inzulínu teda je $0,2 \cdot 75 = 15$ [U] (t.j. 15 000 000 $\mu$U).
Pätnásť jednotiek je podaných hneď na začiatku merania farmakokinetiky a dávka je podaná v priebehu krátkeho času. Budeme uvažovať periódu vzorkovania $T_S = 5$ [min]. „Krátky čas“ je preto 5 minút. Vstup do modelu je v [$\mu$U/kg/min]. Po uvážení všetkého známeho vieme určiť rýchlosť podávania inzulínu takú, že za jednu periódu vzorkovania zodpovedá množstvu 15 U. Označme ju $v_{B}\delta(t) = \frac{15000000}{BW \cdot T_S} = 40000$ [$\mu$U/kg/min] (pričom signál $v_{B}\delta(t)$ na teraz „trvá“ jednu periódu vzorkovania).
V predchádzajúcej časti sme určili bazálnu koncentráciu inzulínu $I_b = 39$ [pmol/l] $= 6,5$ [$\mu$U/ml]. Pre ustálený (bazálny) stav modelu platí $$ \begin{align} S_{2b} &= \frac{k_I \cdot I_b}{ \frac{1}{t_I} \frac{1}{V_I} } \\
S_{1b} &= S_{2b} \\
v_b & = \frac{1}{t_I} S_{1b}
\end{align}$$ Bazálna koncentrácia inzulínu $I_b$ zodpovedá bazálnej rýchlosti podávania inzulínu $v_b = 110,838$ [$\mu$U/kg/min] čo je mimochodom 0,499 [U/h].
Celkový vstup do modelu potom je $v(t) = v_b + v_B \delta(t)$, kde $\delta(t)$ [1/min] je aproximácia Diracovho impulzu pre danú periódu vzorkovania pričom impulz začína v čase podania inzulínu a $v_B = 40000$ [$\mu$U/kg].
Úlohou je nájsť parametre modelu tak, aby sa výstup modelu zhodoval s nameranou farmakokinetikou. V tomto prípade som nepoužil žiadnu slušnú metódu pre hľadanie parametrov (pretože som lenivý, hanba mi) a „od oka“ som modifikoval pôvodné parametre v [1] (hovorme tomu kvalifikovaný odhad). Použité parametre
$$ \begin{align*} t_I &= 51,642 \text{[min]} \\
k_I &= 0,196 \text{[1/min]} \\
V_I &= 87 \text{[ml/kg]}
\end{align*}$$
Výsledok simulácie je na nasledujúcom obrázku:
Celkom dobre takto od oka...
Referencie
| [1] | Pau Herrero, Pantelis Georgiou, Nick Oliver, Monika Reddy, Desmond Johnston, Christofer Toumazou. A composite model of glucagon-glucose dynamics for in silico testing of bihormonal glucose controllers. Journal of Diabetes Science and Technology, July 2013, Volume 7, Issue 4: pages 941-951 |
| [2] | S. R. Mudaliar, F. A. Lindberg, M. Joyce, P. Beerdsen, P. Strange, A. Lin, and R. R. Henry: Insulin aspart (B28 asp-insulin): a fast-acting analog of human insulin: absorption kinetics and action profile compared with regular human insulin in healthy nondiabetic subjects. Diabetes Care September 1999 22:9 1501-1506; doi:10.2337/diacare.22.9.1501 1935-5548 |
MT
30. 5. 2014
Farmakokinetika a farmakodynamika inzulínu - časť 1.
Spôsob merania FK a FD inzulínu
Zjednodušený opis spôsobu merania FK a FD je nasledovný. Máme subjekt bez diabetu. Necháme subjekt pár hodín bez jedla aby sa glykémia ustálila na bazálnej hodnote. Podáme inzulín. Následne pravidelne odoberáme vzorky krvi. Zo vzoriek určujeme koncentráciu inzulínu v krvi a glykémiu. Informácia o glykémii je potrebná pretože zároveň celý čas od podania inzulínu podávame do krvi glukózu tak aby sme udržali glykémiu na pôvodnej bazálnej hodnote. Zaznamenávame rýchlosť prísunu tejto glukózy.Farmakokinetika je jednoducho nameraný časový priebeh koncentrácie inzulínu v krvi. Nameraný časový priebeh rýchlosti podávania glukózy je v tomto prípade farmakodynamika.
Ak by sme nepodávali glukózu do krvi externe, glykémia by po podaní inzulínu klesla. Možno až život ohrozujúco - v závislosti od dávky inzulínu. Podávaním glukózy do krvi tak aby sme udržali glykémiu konštantnú vlastne meriame ako rýchlo sa vplyvom inzulínu stráca glukóza v krvi. Priebeh rýchlosti „strácania sa“ glukózy je farmakodynamika.
Dáta pre model
Aby sme mohli vytvoriť model podľa nameranej FK a FD uvedenej v článku potrebujeme dáta uvedené v článku. Konkrétne dáta z Figure 1A a z Figure 2A. Odčítať z grafu jednotlivé body nie je zásadný problém. Avšak obrázky v publikovanom pdf sú bitmapy. Preto obkreslíme bitmapovú čiaru vektorovou čiarou (v Inkscape v tomto prípade). Potom ľahko získame súradnice bodov vektorovej čiary. Výsledky:
Obr. 1. Prevzaté z [1], Figure 2. Červená čiara je vektorizácia pôvodnej (v tomto .png samozrejme nie...)
SVG dáta čiary (svg m path) obkreslujúcej pôvodné dáta farmakokinetiky sú:
m 32.829958,221.39497 6.818529,-30.80965 6.060916,-67.42769 6.060915,-60.104072 6.565992,-26.263966 6.060915,3.535534 6.565991,1.262691 9.343911,6.313453 9.848988,16.162441 9.343911,16.162441 9.848984,19.697974 18.68783,33.082494 18.68782,30.30458 18.94036,20.20305 18.43528,13.38452 18.94036,9.09137 18.94036,5.80838 18.94036,4.29315 18.68782,4.04061 18.94036,1.51523 18.94036,1.26269 19.1929,1.01015 18.67432,0.49929 18.92858,1.42857 19.10714,0.35715 18.57143,-0.17857 18.75,0.53571
Obr. 2. Prevzaté z [1], Figure 1. Červená čiara je vektorizácia pôvodnej (v tomto .png samozrejme nie...)
m 38.00699,235.4368 6.69226,-1.894 5.808377,-20.83439 6.060916,-36.61803 6.060915,-57.83124 6.313453,-43.43656 6.313454,-4.67195 9.091373,-29.4207 9.596449,2.39912 9.596453,-15.02602 9.47018,8.58629 8.9651,3.03046 9.59645,-6.18718 9.21764,11.99556 9.59645,6.18718 8.9651,19.1929 9.47018,12.62691 9.47018,2.14657 9.47018,6.43973 8.83884,23.86485 9.09137,16.92005 9.84899,14.89975 9.47018,12.37437 9.47018,10.48034 8.83883,6.43972 9.34392,12.37437 9.34391,6.18718 9.09137,8.08122 10.10153,2.27285 9.09137,3.15672 8.83883,2.27285 9.59645,4.41941 9.97526,2.27285 8.5863,1.38896 9.47018,1.51526 9.34391,3.4092 9.59645,1.5153 8.58629,2.0203 9.97526,0.7576 9.09137,1.1364 9.72272,-0.6313 8.83883,0.7576 9.47018,-0.7576
Ako naschvál sú tie obrázky v pdf-ku v takom nízkom rozlíšení, že sa nedajú poriadne prečítať čísla značiek na osiach grafu.
Vieme, že x-ová os (časová os) má rozsah 0 až 600 minút. V Table 1 v [1] sa uvádza, že max hodnota FD profilu je $C_{max} = 813 \pm 23$ [mg/min]. V čase 0 môžme považovať hodnotu FD za nulovú. Max. hodontu FD uvažujme 813 mg/min. V Table 2 v [1] sa píše, že max. hodnota FK je $C_{max} = 501 \pm 111$ [pmol/l]. Prvá číslica na nečitateľnej osi FK grafu vyzerá ako 50. Preto povedzme, že v čase 0 je hodnota FK prfilu rovná 39 pmol/l a maximálna hodnota je 501 pmol/l.
Na základe uvedeného môžme dáta získané vektorizovaním pôvodného grafu previesť na dáta, s ktorými sa dá pracovať ďalej. Výsledok (grafy a tabuľky):
Tabuľka 1.
| čas [min] | FK [pmol/l] | čas [min] | FD [mg/min] | |
| 0.000 | 39.000 | 0.000 | 0.000 | |
| 10.826 | 122.614 | 10.754 | 7.427 | |
| 20.450 | 305.606 | 20.088 | 89.123 | |
| 30.073 | 468.722 | 29.828 | 232.710 | |
| 40.499 | 540.000 | 39.567 | 459.479 | |
| 50.122 | 530.405 | 49.713 | 629.803 | |
| 60.548 | 526.978 | 59.858 | 648.122 | |
| 75.384 | 509.844 | 74.467 | 763.487 | |
| 91.022 | 465.981 | 89.888 | 754.080 | |
| 105.858 | 422.118 | 105.309 | 813.000 | |
| 121.496 | 368.659 | 120.528 | 779.331 | |
| 151.168 | 278.877 | 134.934 | 767.448 | |
| 180.841 | 196.633 | 150.355 | 791.709 | |
| 210.914 | 141.804 | 165.167 | 744.672 | |
| 240.185 | 105.480 | 180.588 | 720.411 | |
| 270.258 | 80.807 | 194.995 | 645.152 | |
| 300.332 | 65.044 | 210.213 | 595.639 | |
| 330.405 | 53.393 | 225.431 | 587.222 | |
| 360.077 | 42.427 | 240.649 | 561.970 | |
| 390.151 | 38.315 | 254.853 | 468.391 | |
| 420.224 | 34.888 | 269.462 | 402.044 | |
| 450.698 | 32.146 | 285.289 | 343.619 | |
| 480.349 | 30.791 | 300.507 | 295.096 | |
| 510.403 | 26.914 | 315.725 | 254.000 | |
| 540.742 | 25.945 | 329.929 | 228.749 | |
| 570.229 | 26.430 | 344.944 | 180.226 | |
| 600.000 | 24.976 | 359.959 | 155.965 | |
| 374.569 | 124.277 | |||
| 390.802 | 115.365 | |||
| 405.411 | 102.986 | |||
| 419.614 | 94.074 | |||
| 435.036 | 76.745 | |||
| 451.065 | 67.832 | |||
| 464.863 | 62.386 | |||
| 480.081 | 56.444 | |||
| 495.096 | 43.076 | |||
| 510.517 | 37.134 | |||
| 524.315 | 29.212 | |||
| 540.345 | 26.242 | |||
| 554.954 | 21.785 | |||
| 570.578 | 24.261 | |||
| 584.782 | 21.290 | |||
| 600.000 | 24.261 |
Referencie
| [1] | S. R. Mudaliar, F. A. Lindberg, M. Joyce, P. Beerdsen, P. Strange, A. Lin, and R. R. Henry: Insulin aspart (B28 asp-insulin): a fast-acting analog of human insulin: absorption kinetics and action profile compared with regular human insulin in healthy nondiabetic subjects. Diabetes Care September 1999 22:9 1501-1506; doi:10.2337/diacare.22.9.1501 1935-5548 |
MT