Bolus wizard je nástroj, pomocou ktorého je možné priamo v pumpe (Medtronic) vypočítať bolus. Bolus wizard pri výpočte bolusu vyhodnocuje aj tzv. aktívny inzulín - inzulín, ktorý ešte účinkuje od posledného bolusu, zostatkový inzulín, „insulin on board“...
Pre výpočet aktívneho inzulínu sa používa krivka aktívneho inzulínu. Dáva do vzťahu čas od podania bolusu a množstvo inzulínu, ktoré akoby ostáva, ktorého účinok sa ešte prejaví.
Narýchlo vygooglené letáky hovoria o krivke aktívneho inzulínu nasledovné:
Krivka vyzerá nasledovne:
Manuál pumpy Paradigm 522 obsahuje aspoň trošku lepší obrázok krivky aktívneho inzulínu:
Manuál odkazuje na článok autorov Mudalair a kol., ktorý už poznáme zo štúdia farmakodynamiky. Údajne graf krivky v manuály je adaptáciou z uvedeného článku. Žiadny podobný graf sa pritom v článku nenachádza. Viem si však zhruba predstaviť čo vyjadruje krivka aktívneho inzulínu vo vzťahu k farmakodynamike inzulínu prezentovanej v uvedenom článku.
Krivku aktívneho inzulínu je možné aj odmerať. Myslím tým jednoducho sledovať údaj „aktívny inzulín“ v pumpe po boluse. „Meral“ som nasledovne. Manuálne (nie pomocou bolus wizardu) som podal bolus 5 U. Potom som v pravidelných intervaloch „otvoril“ bolus wizard, pozrel hodnotu údaja aktívny inzulín a zapísal spolu s časom. Odmeral som krivku pre jej tri rôzne nastavenia - dĺžky účinku inzulínu. Konkrétne „active insulin time“ 2 hod., 4 hod. a 6 hod (8 hodín sa mi nechcelo čakať). Meranie prebehlo na pumpe Paradigm 522 (pre mňa veľmi vzácnej). Starší typ ale novšie pumpy sú myslím v tomto také isté. Nie, pumpa počas „merania“ nebola k nikomu pripojená.
Namerané krivky sú na nasledujúcom obrázku. 100 % množstva inzulínu je v tomto prípade 5 U.
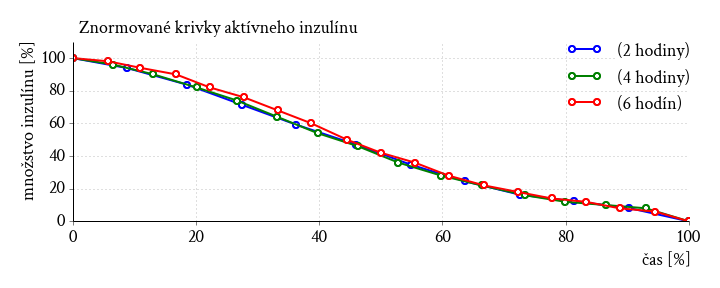
Jednoznačne sa to podobá na to čo je uvedené v manuáli. Ak znormujeme čas všetkých nameraných kriviek na 0 až 100 % vidíme, že tie krivky sú rovnaké čo sa tvaru týka:
Z tvaru krivky sa dá usúdiť, že matematickým predpisom, ktorý vystihuje krivku by mohla byť polynomiálna funkcia s polynómom 3. stupňa.
$$
\begin{align*}
y &= f(x) \\
y &= p_3 x^3 + p_2 x^2 + p_1 x + p_0
\end{align*}
$$
Podľa obrázku vyššie môžme celkom logicky žiadať aby $100 = f(0)$, $50=f(50)$ a $0 = f(100)$. Z toho nie práve očividne, ale predsa vyplýva, že pomyselná ideálna krivka môže byť daná parametrami $p_3=2e-4$, $p_2=-3e-2$, $p_1 = -9e-4$ a $p_0 = 100$ (pre analytické odvodenie by sme uvažovali aj požiadavky na deriváciu $f'(x)$ atď.), teda:
$$
f_{ideal}(x) = 0.0002 x^3 - 0.003 x^2 - 0.0009 x + 100
$$
Parametre modelu krivky je samozrejme možné získať aj v zmysle metódy najmenších štvorcov (regresnou analýzou). Výsledkom je
$$
f_{model}(x) =1.26 \cdot 10^{-4} x^3 -1.495\cdot 10^{-4} x^2 -7.46\cdot 10^{-4}x + 101.81
$$
Graficky sú tieto funkcie porovnané s nameranými dátami na nasledujúcom obrázku. Samozrejme „model“ lepšie vystihuje namerané dáta ako vymyslená ideálna krivka.
Majúc aproximáciu krivky aktívneho inzulínu, všeličo by sa dalo robiť. Možno niekedy nabudúce.
MT
p.s. Tento krát je font pre text v grafoch zavedený konečne inteligentne... Stačilo súbor fontu dať medzi ostatné fonty matplolib-u (to som mal aj pred tým) a potom vymazať súbor ~/.matplotlib/fontlist.cache. Následne po importe matplotlib-u si tento všimne, že tam ten súbor chýba a vyrobí nový. Nový súbor už obsahoval aj info o novom fonte, pretože ho našiel v adresári. Konečne stačilo štandardne zmeniť rc parameter font.family a veselo používať nový font.